
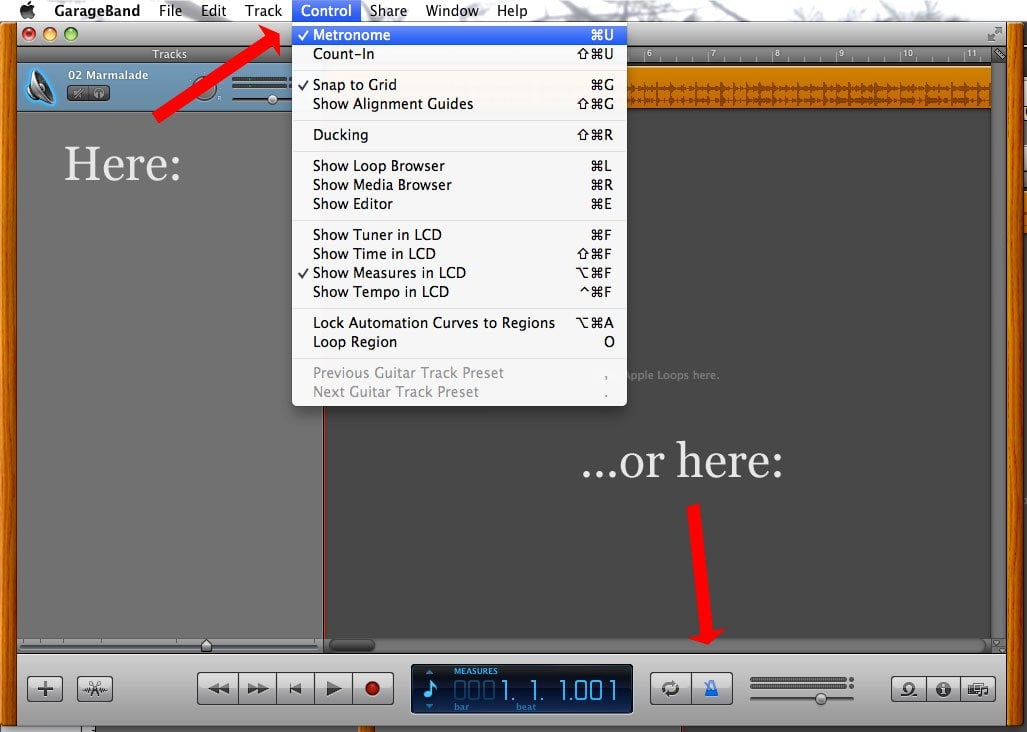
- #How to change pitch in garageband 10.1 6 how to#
- #How to change pitch in garageband 10.1 6 download#
(browse pane -> vocals (left side) -> and specific vocal type (right side)). Just select one of the preset vocal settings. Echoing Gjmnz, a preset is a good place to start. I still believe that its a decent method, even though there are several flaws or unneces. Types: 01, Beat, Blush, Cleats, Education, Criminal und meh Info Pane, then choose different vocal effects settings while singing and. If you're new to be able to GarageBand and the process of recording vocals. each of these and tweak these settings and / or add more effects upon top in which will to create something unique. For now, choos GarageBand Tutorial - Vocal Effects - Sidebar.

Again, this is a matter of taste and you can always change the effects setting after recording. So, with the track selected, click on Vocals in the right side of the Browse tab in the Track Info Pane, then choose different vocal effects settings while singing and listening to the results.

#How to change pitch in garageband 10.1 6 download#
Uncategorized Download my free Ultimate Vocal Preset Bundle.

Using Presets to make gorgeous vocals with GarageBand. About Blog FREE VOCAL PRESETS Coaching Login.
#How to change pitch in garageband 10.1 6 how to#
Attack: 1 ms or less We walk through how to find the perfect vocal compression setting, how to pick an EQ preset while looking out for muddy frequencies, and how to add saturation to truly make your vocals sound gorgeous. It's designed to bring the Vocal track to the forefront of your mix - take care not to over squash your audio! Threshold: -2 to -5 dB 1 ms or less. Rossing also reports that the critical bandwidth (related to loudness perception) is about 30 times the jnd for pitch, suggesting that both are related to the regions of excitation along the basilar membrane of the inner ear.Unlike the last 'recipe', the purpose of these settings is to really let you hear the compressor at work. The real world can rarely be accurately characterized by simple rules. He also states that the jnd has been found to depend upon the frequency, the sound level, the duration of the tone, the suddenness of the frequency change, the musical training of the listener, and the method of measurement. The jnd is found to be about 0.5% of the pure tone frequency, which corresponds to about 8¢. Rossing describes measurements of pitch discrimination with pure tones at about 80 dB for frequencies between 1 and 4 kHz. One of the advantages of the cents notation is that it expresses the same musical interval, regardless of the frequency range.Įvaluating the just noticeable difference in pitch by the "nickel's worth" rule is convenient, but as you might expect it is an oversimplification. Although research reveals variations, a reasonable estimate of the JND is about five cents. It is convenient to express the just noticeable difference in cents since that notation was developed to express musical intervals. The just noticeable difference in pitch must be expressed as a ratio or musical interval since the human ear tends to respond equally to equal ratios of frequencies. Note that the range represented by 5¢ increases from less than a tenth of a Hz at the low end of the piano to about 10 Hz at the top end of the piano. Included with the semitone intervals above is an evaluation of the deviation in Hz needed to equal 5¢, the nominal just-noticeable difference for these pitches. The interval value in cents expresses the ratio of the frequencies, which is the same for every equal tempered semitone. Expressed in Hz difference, every semitone is different. Taking the log of both sides gives:Įxamining the semitone A to B-flat at different points in the range of the piano will illustrate the fact that if expressed in cents, every equal tempered semitone is the same. To calculate the number of cents for any two frequencies, the above relationship must be reversed. This is convenient for calculating the frequency corresponding to a certain number of cents. The fact that one octave is equal to 1200 cents leads one to the power of 2 relationship: If f 1 = Hz and f 2 = Hz then the interval is cents. An octave is then 1200¢ and the other equal tempered intervals can be obtained by adding semitones: Musical intervals are often expressed in cents, a unit of pitch basedupon the equal tempered octave such that one equal tempered semitone is equal to 100 cents. The Use of Cents for Expressing Musical Intervals Cents


 0 kommentar(er)
0 kommentar(er)
